Some Amusing Illustrations of Conformal Maps

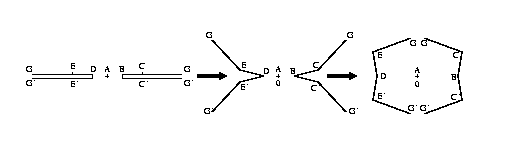
Illustrations The following are conformal maps or illustrations associated with the mapping of the upper half plane into rectangles.

Foldover This shows the plane with slits from negative infinity to -1 and from +1 to positive infinity being folded up into a rectangle.

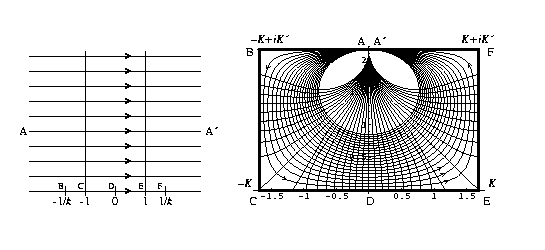
Dipole Field On the left this shows a flow in the plane from a positron at - infinity to an electron at + infinity. On the right is the field of a dipole (positron on left, electron on right) at the center top of a piece of tinfoil. The conformal map here is given by the Jacobi Ellipitic sine g(z)=sn(z,k).

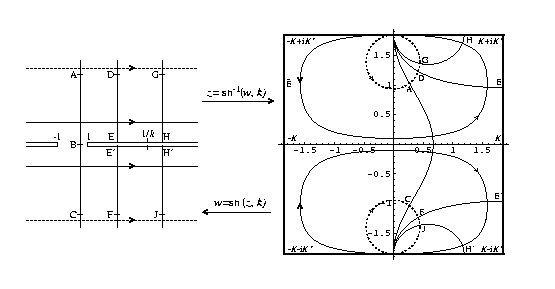
Dipole Field Again This is the same as the last but concentrating on the mathematical features of the map.

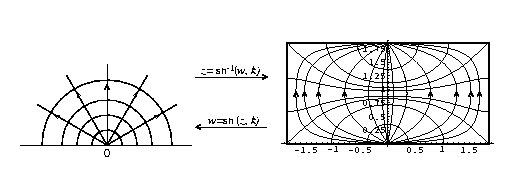
Field of Charge at Top and Bottom On the left this shows a radial flow out of the origin (a positron at the origin and an electron at infinity). On the right is the flow from a positron at the center bottom of a piece of tinfoil toward an electron at the center top of the tinfoil.

NAU Home Page Department of Mathematics Schulz Home Page